Intégrales simples

	exercices résolus d'integrales  exercices résolus: integrales simples Intégrales généralisées Intégrales multiples Intégrales curvilignes Intégrales de surface calcul des intégrales: exercices avec solustion exercices résolus d'integrales généralisées Exercice 1
	Calculer les primitives suivantes :
	Exercice 2
	Calculer les primitives suivantes :
	Exercice 3
	Calculer les primitives suivantes :
	Exercice 4
	Calculer les primitives suivantes :
	Exercice 5
	Calculer les primitives suivantes :
	Exercice 6
	Calculer les primitives suivantes :
	Exercice 7
	Calculer les primitives suivantes :
	Exercice 8
	Calculer les primitives suivantes :
	Exercice 9
	Calculer les primitives suivantes :
	Exercice 10
	Calculer les primitives suivantes :
	Exercice 11
	Calculer les primitives suivantes :
	Exercice 12
	Calculer les primitives suivantes :
	Exercice 13
	Exercice 14
	Exercice 15
	Exercice 16

Intégrales  - Réponses
	Exercice 1 - Réponse
	Exercice 2 - Réponse
	Exercice 3 - Réponse
	Exercice 4 - Réponse
	Exercice 5 - Réponse
	RAPPEL Primitivation par parties: N'introduire la constante qu'à la fin du calcul On intègre une seconde fois par parties en posant toujours u égal au polynôme pour abaisser son degré
	Exercice 6 - Réponse
	La fonction  est transcendante et sa dérivée est algébrique. On intègre par parties en posant u égal au logaritme. La fonction  est transcendante et égale à sa dérivée. On intègre par parties en posant u égal à l'exponentielle. On intègre une seconde fois par parties
	Exercice 7 - Réponse
	On intègre par parties deux fois de suite et "dans le même sens" par exemple On intègre une seconde fois par parties Equation permettant d'obtenir le résultat On peut également procéder par dérivation puis par identification. On pose à priori le résultat sous la forme On dérive et on identifie
	Exercice 8 - Réponse
	Exercice 9 - Réponse
	m impair m pair p impair t= sinx ou t=cosx t= sinx p pair t=cosx linearisation(Euler)
	Exercice 10 - Réponse
	On intègre par parties
	Exercice 11 - Réponse
	Exercice 12 - Réponse
	VOIR LE CHAPITRE FRACTIONS RATIONNELLES on décompose en éléments simples les fractions rationnelles
	Exercice 13 - Réponse
	Exercice 14 - Réponse
	Exercice 15 - Réponse
	Exercice 16 - Réponse
	Exercice 17 - Réponse
	Exercice 18 - Réponse
	Exercice 19 - Réponse
	Exercice 20 - Réponse
	Exercice 21 - Réponse
	Exercice 22 - Réponse

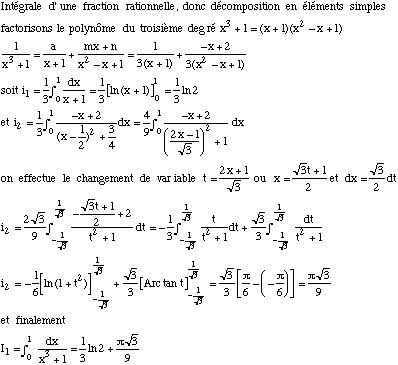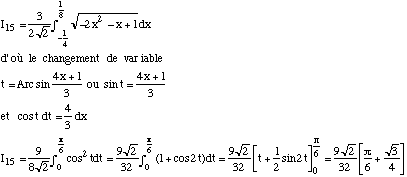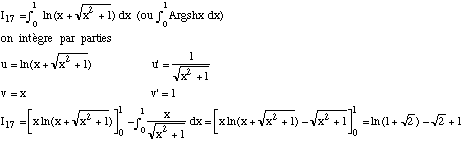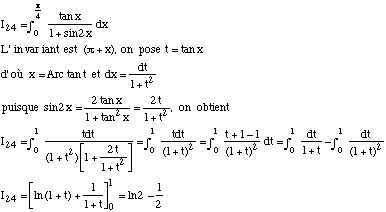source de ses exercices est le site : http://maths54.free.fr